Detect and Measure Gerrymandering
Metric for detecting gerrymandering
Abstract from the publication
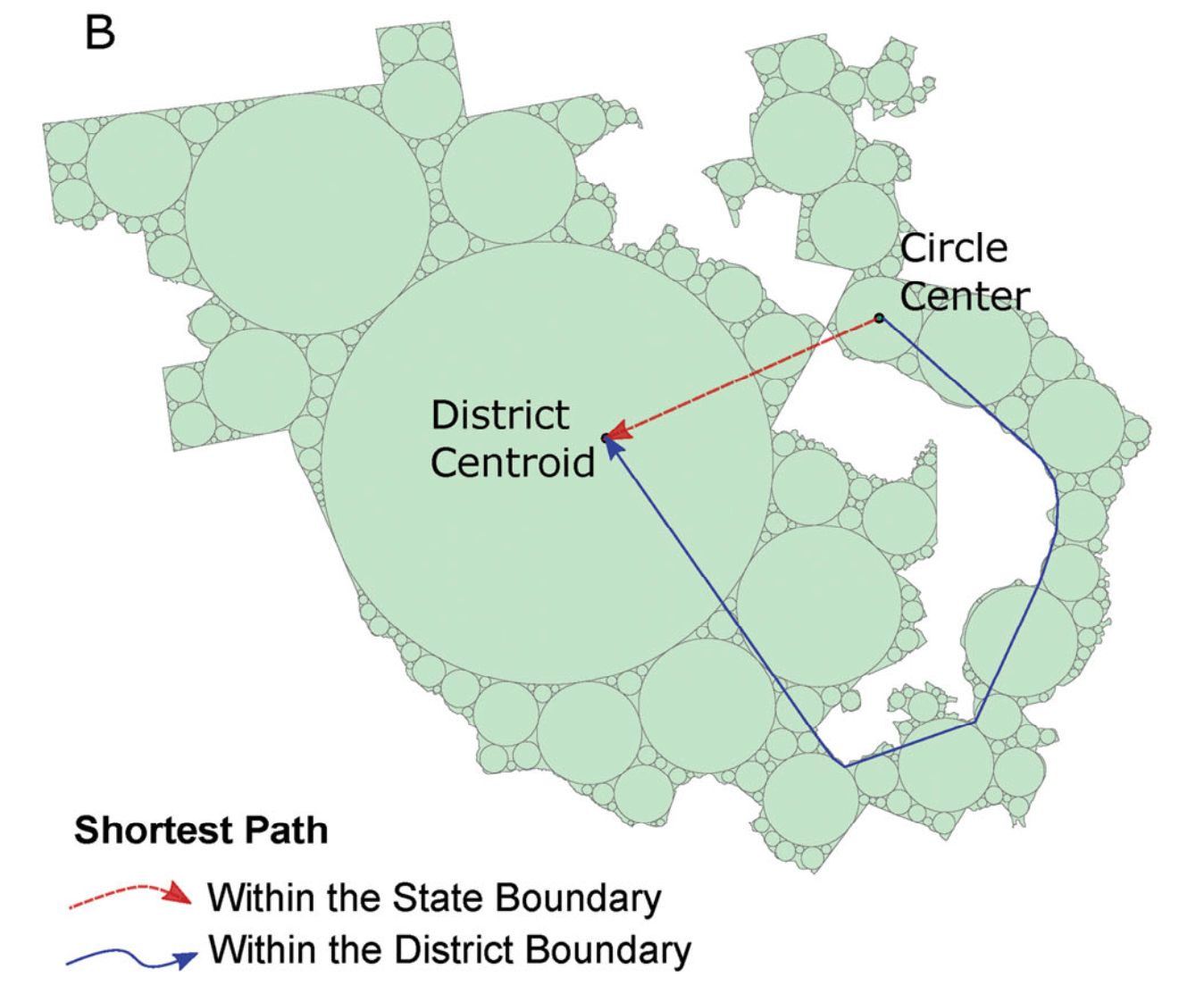
Measuring the form and structure of geographic landscapes is fundamental to understanding geospatial phenomena and their dynamics. Shape compactness metrics have been extensively employed in gerrymandering assessment, urban planning, landscape ecology, and other applications. Existing compactness measurements for gerrymandering, however, target particular aspects of gerrymandered shapes such as elongation, indentation, or dispersion without adequately integrating them with spatial context. This article proposes a comprehensive shape compactness metric that coherently integrates these aspects. It first divides a district into nonoverlapping maximum inscribed circles. Then Euclidean distances from the centers of these circles to the district centroid are standardized and regulated using contextual and topological factors like the distribution of attributes, the fixed upper level boundary, and the relationships with other districts. Finally, these regulated distances are aggregated to produce a quantitative compactness measure that, unlike most existing ones, features a threshold for gerrymandering identification and the coherent integration of roundness, convexity, closeness, and spatial context. Applying the new metric to the U.S. Congressional districts exemplifies its differences from existing metrics and also illustrates the necessity and value of coherently combining multiple aspects of gerrymandering in a single shape compactness metric.
References
Sun, S. (2020). Developing a Comprehensive and Coherent Shape Compactness Metric for Gerrymandering. Annals of the American Association of Geographers, 1-21. https://doi.org/10.1080/24694452.2020.1760779
Sun, S. (2023, June 28-30). Redrawing electoral maps to curb gerrymandering: a case study of New York State in 2022. 5th International Conference on Advanced Research Methods and Analytics (CARMA 2023), Servilla, Spain. https://doi.org/10.4995/CARMA2023.2023.16481